Out in the Middle of Space

🔖 Background Information

You have probably worked with the Cartesian coordinate system where the coordinates of a point are given by its distance along the x-axis, its distance along the y-axis, and its distance along the z-axis.

$$p=(x,y,z)$$

However, this is not the only way that we could define a point in space. In some problems, it makes sense to use spherical coordinates. With a spherical coordinate system, you measure a point in space by its distance from the origin (r), the angle that you rotate around the z-axis ($\theta$), and the distance you rotate down from the z-axis ($\varphi$).

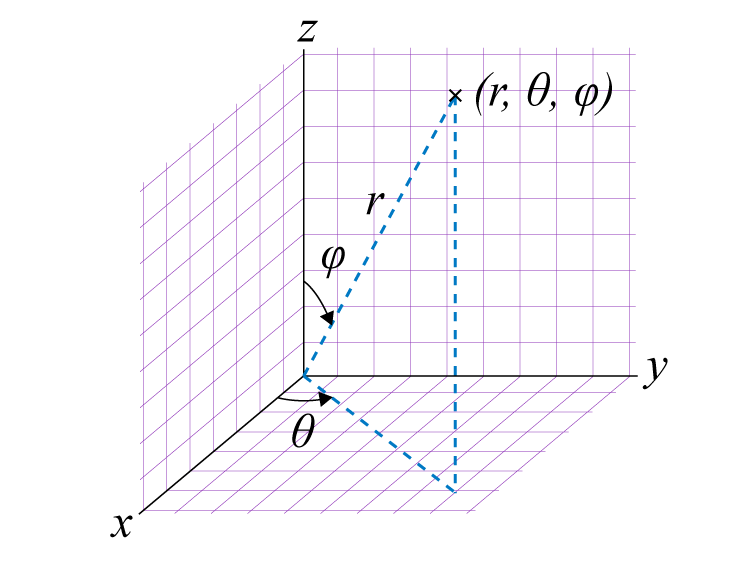
This image comes courtesy of Byju (BYJU, n.d.).

There is nothing special about one system or another. It’s like measuring a distance in miles versus kilometers - as long as you are consistent with your system, you will get the same answer at the end of the day.

You can convert from Cartesian coordinates to spherical coordindates using the following formulas:

$$r^2=x^2+y^2+z^2$$ $$\theta =ta{n}^{-1}\left(\frac{y}{x}\right)$$ $$\varphi =co{s}^{-1}\left(\frac{z}{r}\right)$$

You can convert from spherical coordinates to Cartesian coordindates using the following formulas:

$$x=rcos\theta sin\varphi$$ $$y=rsin\theta sin\varphi$$ $$z=rcos\varphi$$

🎯 Problem Statement

Create a program that allows a user to input a set of Cartesian or spherical coordinates. Then, it converts those coordinates to the other system.

✅ Acceptance Criteria

• When I start the program, I should see a welcome message.
• The program should ask if I want to enter three spherical coordinates or three Cartesian coordinates. I should be able to make a selection and enter my coordinates.
• After I enter my coordinates, the program should print them out, both in the Cartesian and spherical systems.
• Finally, the program should display a message and exit gracefully.

As an additional requirement for this lab, you must put the logic of converting from one coordinate system to the other in one or more functions. You cannot write the logic for the conversion directly in main(). The logic for I/O (cin and cout) can live in main(), if you would like.

📋 Dev Notes

• Think about which functions might be useful to define for the conversions. One function per coordinate? One function that converts and prints out all of the coordinates? Both?
• You can represent the angles in either radians or degrees. Just be sure to specify which one you used in your program.
• You can assume that the user will always choose spherical or Cartesian coordinates. You do not have to implement validation logic (that is an optional add-on for the portfolio if you would like to tackle it).

🖥️ Example Output

./space.out
 
Welcome to the Point Conversion Program!
 
Do you want to enter your coordinate in:
 
(1) Spherical Coordinates
(2) Cartesian Coordinates
 
2
 
Enter your coordinates, separated by spaces:
 
12 10 0
 
Your point is as follows. Angles are in radians:
 
Spherical Coordinates: (15.6, 0.7, 1.6)
Cartesian Coordinates: (12, 10, 0)
 
Thank you for using the Point Conversion Program!

📝 Thought Provoking Questions

1. Which functions did you define for the conversion from one coordinate system to the other?
2. Do you pass arguments by reference or value in your functions. Why did you make that choice?

💼 Add-Ons For the Portfolio

(One Credit) Validation of User’s Choice

When prompted to select either spherical or Cartesian coordinates, users might make a selection that is neither of those two options. Add in some validation logic that checks their input and re-prompts them for a value if it is invalid. Otherwise, the program should run as it did before.

Some example output might look like this:

./space.out
 
Welcome to the Point Conversion Program!
 
Do you want to enter your coordinate in:
 
(1) Spherical Coordinates
(2) Cartesian Coordinates
 
3
 
That is not a valid choice!
 
Do you want to enter your coordinate in:
 
(1) Spherical Coordinates
(2) Cartesian Coordinates
 
2
 
Enter your coordinates, separated by spaces:
 
12 10 0
 
Your point is as follows. Angles are in radians:
 
Spherical Coordinates: (15.6, 0.7, 1.6)
Cartesian Coordinates: (12, 10, 0)
 
Thank you for using the Point Conversion Program!

🔗 Useful Links

N/A

📘 Works Cited

BYJU. (n.d.). Spherical Coordinates-Definition and Conversions. In BYJU’S. Retrieved March 17, 2024, from https://byjus.com/maths/spherical-coordinates/